Conversion between image and world coordinates

Conversion between Image Coordinates and World Coordinates are fundamental to all image formation problems. Always confused to me. Sumup here for further references.

Preknowledge: Camera calibration information

First we have to know camera calibration information, which is essential for these conversions. These parameters contains (see PETS 2009’s calibration data as an example):

1. Geometry parameters

• \(w\), \(h\) (image’s width and height)
• \(dpx\), \(dpy\)
• \(dx\), \(dy\)
• \(ncx\)
• \(nfx\)

2. Intrinsic parameters

• \(f\) (focal length)
• \(sx\)
• \(cx\), \(cy\)
• \(kappa1\)

3. Extrinsic parameters

• \(rx\), \(ry\), \(rz\)
• \(tx\), \(ty\), \(tz\)

Based on above parameters, we can get:

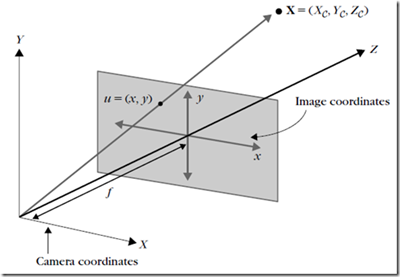
1. Camera transform matrix \(Pc\) (3×4) that multiplies a scene point expressed as a homogeneous coordinate in \(R^4\) (\(w1(x,y,z,1)\)) to produce an image point expressed as a homogeneous coordinate in \(R^3\) (\(w2(u,v,1)\)).

   NOTE: Traditionally, we can obtain (u,v) by the following formula that is projected from 3D scene point (x,y,z). But we have to concern image distortion problem, thus, in practice, we often do this by 4 steps as shown in following PART: World coordinates to image coordinates.

   $$w \begin{pmatrix} u \\\ v \\\ 1 \end{pmatrix} = Pc \cdot \lambda \begin{pmatrix} x \\\ y \\\ z \\\ 1 \end{pmatrix} = \begin{pmatrix} R11 & R12 & R13 & R14 \\\ R21 & R22 & R23 & R24 \\\ R31 & R32 & R33 & R34 \end{pmatrix} \cdot \lambda \begin{pmatrix} x \\\ y \\\ z \\\ 1 \end{pmatrix}$$

   , where

   $$\begin{cases} \begin{array}{l l} R11 &= cb \cdot cg \\\ R12 &= cg \cdot sa \cdot sb - ca \cdot sg \\\ R13 &= sa \cdot sg + ca \cdot cg \cdot sb \\\ R14 &= tx \\\ R21 &= cb \cdot sg \\\ R22 &= sa \cdot sb \cdot sg + ca \cdot cg \\\ R23 &= ca \cdot sb \cdot sg - cg \cdot sa \\\ R24 &= ty \\\ R31 &= -sb \\\ R32 &= cb \cdot sa \\\ R33 &= ca \cdot cb \\\ R34 &= tz \\\ sa &= \sin(rx) \\\ ca &= \cos(rx) \\\ sb &= \sin(ry) \\\ cb &= \cos(ry) \\\ sg &= \sin(rz) \\\ cg &= \cos(rz) \end{array} \end{cases}$$

2. Camera position (\(C{posx}\), \(C{posy}\), \(C_{posz}\)):

   $$\begin{cases} \begin{array}{l l} Cposx &= -( tx \cdot R11 + ty \cdot R21 + tz \cdot R31 ) \\\ Cposy &= -( tx \cdot R12 + ty \cdot R22 + tz \cdot R32 ) \\\ Cposz &= -( tx \cdot R13 + ty \cdot R23 + tz \cdot R33 ) \end{array} \end{cases}$$

World coordinates to image coordinates (\(3D=>2D\), i.e., \((x,y,z)=>(u,v)\))

Meaning: 3D scene point \((x,y,z) =>\) 2D image pixel \((u,v)\). There need to be 4 steps to do this:

1. Convert from world coordinates to camera coordinates (\(3D => 3D\), i.e., \((x,y,z)=>(xc,yc,zc)\)):

   $$\begin{pmatrix} xc \\\ yc \\\ zc \end{pmatrix} = Pc \cdot \begin{pmatrix} x \\\ y \\\ z \\\ 1 \end{pmatrix}$$

2. Convert from camera coordinates to undistorted sensor plane coordinates (\(3D=>2D\), i.e., \((xc,yc,zc)=>(xu,yu)\)):

   $$\begin{cases} \begin{array}{l l} xu &= \frac{f \cdot xc}{zc} \\\ yu &= \frac{f \cdot yc}{zc} \end{array} \end{cases}$$

3. Convert from undistorted to distorted sensor plane coordinates (\(2D=>2D\), i.e., \((xu,yu)=>(xd,yd)\)), reference to the following function in PETS 2009’s calibration pragram:

   void CameraModel::undistortedToDistortedSensorCoord (double Xu, double Yu, double& Xd, double& Yd)

4. Convert from distorted sensor plane coordinates to image coordinates (\(2D=>2D\), i.e., \((xd,yd)=>(u,v)\)):

   $$\begin{cases} \begin{array}{l l} u &= \frac{xd \cdot sx}{dpx} + cx \\\ v &= \frac{yd}{dpy} + cy \end{array} \end{cases}$$

Image coordinates to world coordinates (\(2D=>3D\), i.e., \((u,v)=>(x,y,z)\))

NOTE: If we only have one view, we actually can not get this done unless we also know its z-axis. In this case, please refer to the following function in PETS 2009’s calibration pragram:

bool CameraModel::imageToWorld(double Xi, double Yi, double Zw, double& Xw, double& Yw)

Or we can use multi-views to make this done. The following are the steps given two image coordinates from two different views \((u1,v1)(u2,v2)\), both of them are projected from the same 3D scene point \((x,y,z)\). In this case, the problem has changed to be 2 \(2D\) pair points (corresponding points) \(=> 3D\), i.e., \((u1,v1)(u2,v2)=>(x,y,z)\).

The idea is that we anti-project to the \(3D\) space (See following figure, \(C1,C2\) are the camera positions and \(p1=(u1,v1)\), \(p2=(u2,v2))\). We based on line \(R1=C1p1\) and line \(R2=C2p2\). Perfectly, the intersection of \(R1\) and \(R2\) is what we want \(P(x,y,z)\). Unfortunately, \(R1\) and \(R2\) do not in practice intersect, then the idea changes to find midpoint of shortest perpendicular. The following are the steps: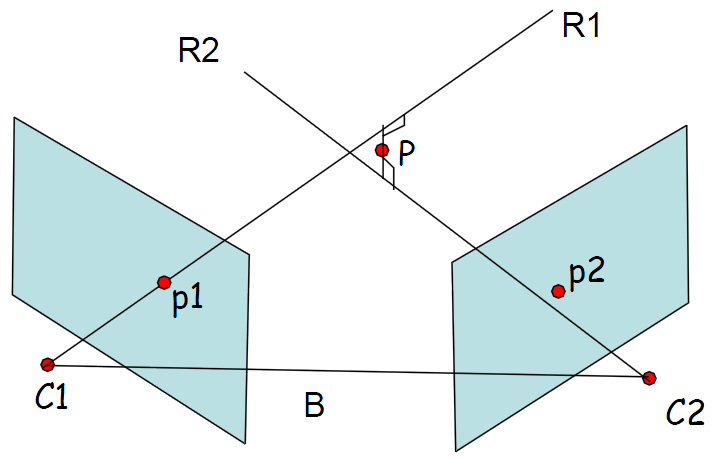

1. Convert from image coordinates to distorted sensor coordinates (\(2D=>2D\), i.e., \((u1,v1)=>(xd1,yd1), (u2,v2)=>(xd2,yd2)\)):

   $$\begin{cases} \begin{array}{l l} xd1 &= dpx \cdot \frac{u1 - cx1}{sx1} \\\ yd1 &= dpy \cdot (v1 - cy1) \\\ xd2 &= dpx \cdot \frac{u2 - cx2}{sx2} \\\ yd2 &= dpy \cdot (v2 - cy2) \end{array} \end{cases}$$

2. Convert from distorted sensor to undistorted sensor plane coordinates (\(2D=>2D\), i.e., \((xd1,yd1)=>(xu1,yu1), (xd2,yd2)=>(xu2,yu2)\)):

   $$\begin{cases} \begin{array}{l l} xu1 &= xd1 \cdot (1 + kappa11 \cdot (xd1 \cdot xd1 + yd1 \cdot yd1)) \\\ yu1 &= yd1 \cdot (1 + kappa11 \cdot (xd1 \cdot xd1 + yd1 \cdot yd1)) \\\ xu2 &= xd2 \cdot (1 + kappa12 \cdot (xd2 \cdot xd2 + yd2 \cdot yd2)) \\\ yu2 &= yd2 \cdot (1 + kappa12 \cdot (xd2 \cdot xd2 + yd2 \cdot yd2)) \end{array} \end{cases}$$

3. Convert from undistorted sensor plane coordinates to camera coordinates (\(2D=>3D\), i.e., \((xu1,yu1)=>(xc1,yc1,zc1), (xu1,yu1)=>(xc1,yc1,zc1)\)):

   $$\begin{cases} \begin{array}{l l} xc1 &= xu1 \\\ yc1 &= yu1 \\\ zc1 &= f1 \\\ xc2 &= xu2 \\\ yc2 &= yu2 \\\ zc2 &= f2 \end{array} \end{cases}$$

   NOTE: Here assumed that image plane are between camera position and the scene, if are not, \(zc\) should be set to be \(–f\).

4. Convert from camera coordinates to world coordinates (\(3D=>3D\), i.e., \((xc1,yc1,zc1)=>(x1,y1,z1), (xc2,yc2,zc2)=>(x2,y2,z2)\)): refer to the following function in PETS 2009’s calibration pragram:

   bool CameraModel::cameraToWorldCoord (double xc, double yc, double zc, double& xw, double& yw, double& zw)

5. Compute closest pair points of pair camera rays, say M1M2.
6. Return M1M2’s midpoint as result.

References

1. Multi-Camera Networks: Principles and Applications, H. Aghajan, A. Cavallaro, Elsevier, ISBN: 978-0-12-374633-7, May 2009.
2. PETS 2009 Benchmark Data, http://www.cvg.rdg.ac.uk/PETS2009/a.html.